Color Cube Meets Rubik’s Cube
I have made a half dozen blog posts about Rubik's Cube so far this year. And, during the MATLAB Central Mini Hack in October, I resurrected an old code about the Color Cube. Now, a combination of the two, Rubik/Color Qube, creates an elegant tool for investigating Matrices in Action.
Contents
Opening
Here is the opening screen shot of Rubik/Color Qube, one of the most elaborate MATLAB programs that I have ever written.
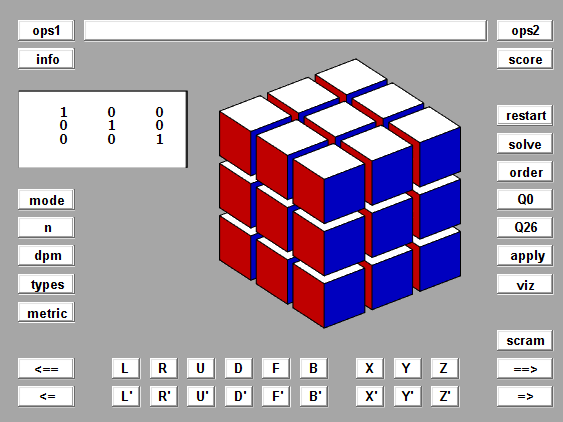
Rubik and Color
There are two modes, rubik and color. In rubik mode, the large cube is formed from 27 identical copies of a single small cubelet. The six cubelet faces have six different colors. Red, white and blue are visible initially. Orange, yellow and green become visible as the faces are rotated.

In color mode, the large cube is formed from 27 cubelets, each with a different solid color. Three of the corner cubelets are the primary colors in the RGB color model -- red, green and blue. Three more corners are the complementary cyan, magenta and yellow. White and black complete the list of corners.

Color Qube
All of the familiar Rubik's moves are available in color mode. Here is a screen shot after a few rotations.
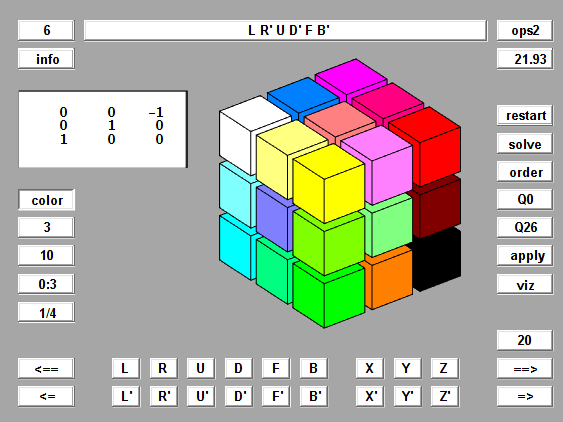
Rotations
Rotation matrices defined by this Rk function are the basic mathematical tool employed by Qube. The animation provides a detailed look at the action produced by the F key, counter-clockwise rotation of the Front face. This is the y-axis, case 2 in Rk. The detail is provided by taking d = 0:3:90, so there are 30 steps of 3 degrees.
function R = Rk(axis,d) % Rk(axis,d), Rotation by d degrees about the x-, y-, or z-axis. c = cosd(d); s = sind(d); switch axis case 1, R = [ 1 0 0 0 c s 0 -s c ]; case 2, R = [ c 0 s 0 1 0 -s 0 c ]; case 3, R = [ c s 0 -s c 0 0 0 1 ]; end fmat = findobj('tag','fmat'); if ~isempty(fmat) fmat.String = mat3(R); end end
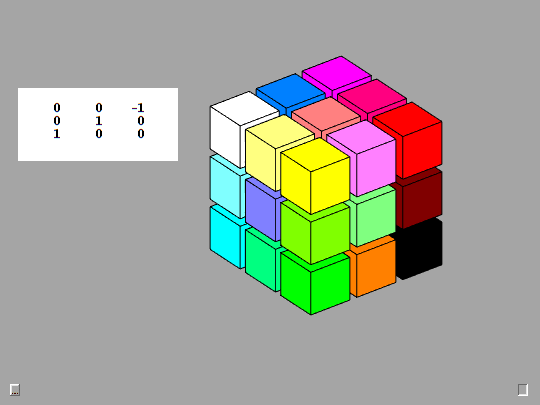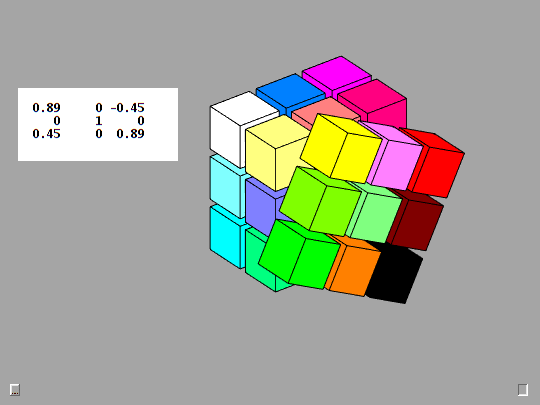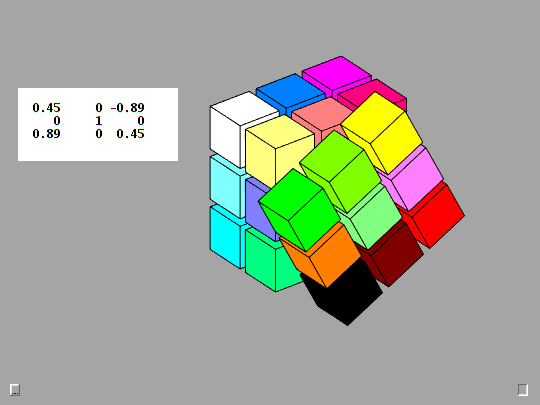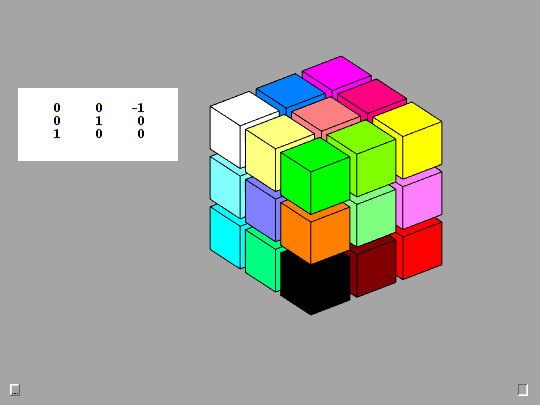
n-by-n-by-n
Qube generalizes the classic 3-by-3-by-3 Rubik's Cube to n-by-n-by-n cubes for any n.
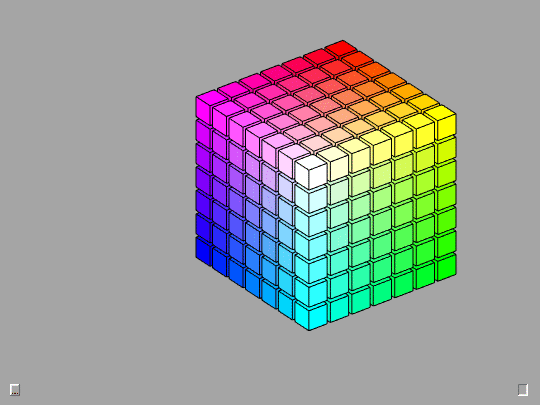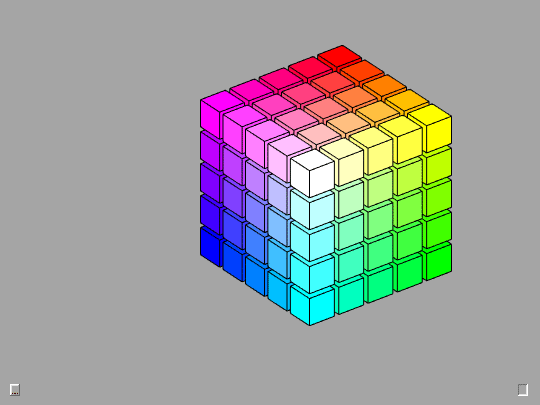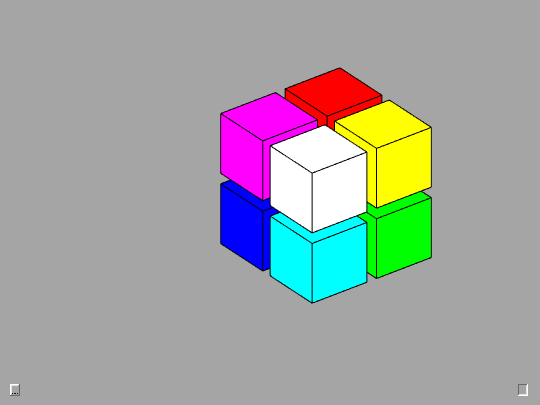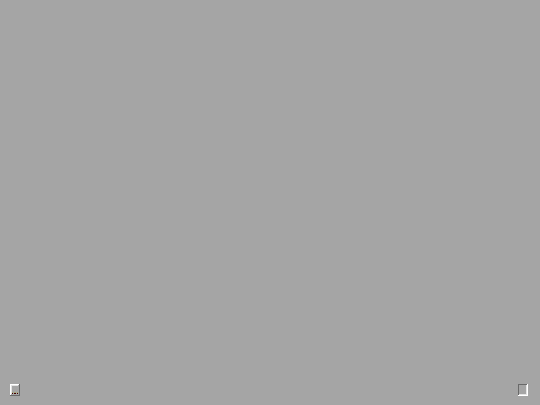
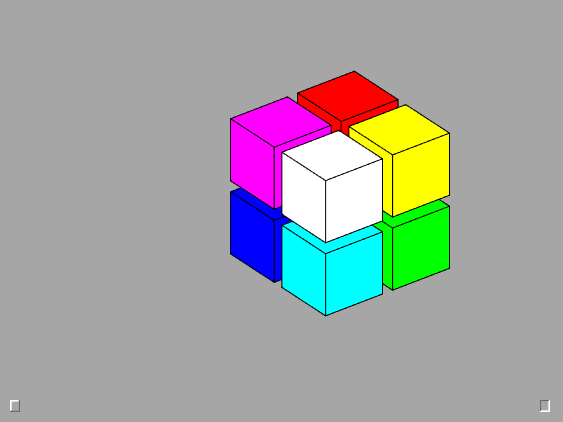
2-by-2-by-2
The 2-by-2-by-2 cubes are good starting points for investigation of mathematical properties.

Software
Qube is available as a self-extracting MATLAB archive at this link, Qube_mzip.m.
Get
the MATLAB code
Published with MATLAB® R2022b
