An Interesting, and Perhaps New, Matrix

I do not recall having seen this matrix before, but I will not be surprised to learn that somebody else already knows all about it, especially if that person's name is Nick.

Contents

Q

I've been investigating the matrices generated by this elegant one-liner.

    Q = @(n) (-n:n).^2 + (-n:n)'.^2;

The Q is for "quadratic".

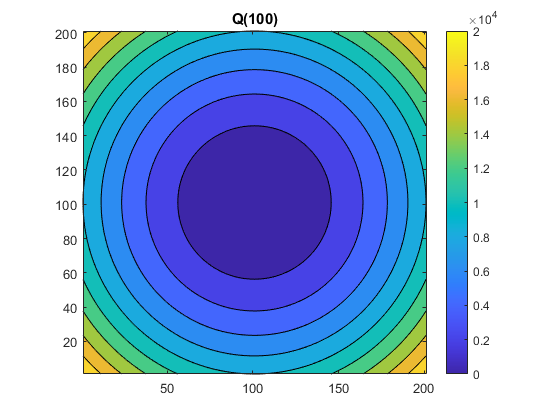
The middle column contains the squares of the integers from -n to n. So does the middle row. The apostrophe summons singleton expansion. The resulting matrix has order 2*n+1. Here is Q(5).

    Q5 = Q(5)

Q5 =

    50    41    34    29    26    25    26    29    34    41    50
    41    32    25    20    17    16    17    20    25    32    41
    34    25    18    13    10     9    10    13    18    25    34
    29    20    13     8     5     4     5     8    13    20    29
    26    17    10     5     2     1     2     5    10    17    26
    25    16     9     4     1     0     1     4     9    16    25
    26    17    10     5     2     1     2     5    10    17    26
    29    20    13     8     5     4     5     8    13    20    29
    34    25    18    13    10     9    10    13    18    25    34
    41    32    25    20    17    16    17    20    25    32    41
    50    41    34    29    26    25    26    29    34    41    50

I like the contour plot.

    contourf(Q(100))
    axis square
    colorbar
    title('Q(100)')

D

For another blog post under development, I need a logical mask that carves a circular region out of graphic. This disc does the job.

    D = @(n) Q(n) <= n^2;

Here is my carver.

    spy(D(100))
    title('D(100)')

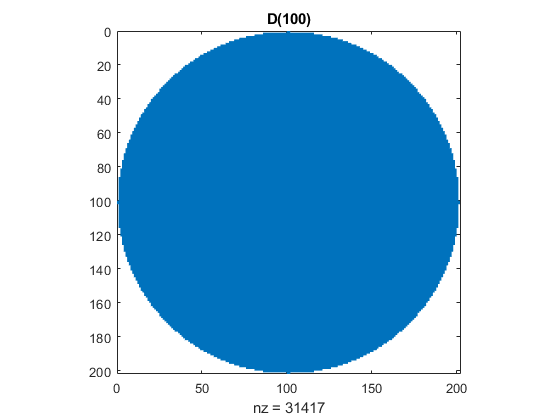
Did you notice the digits in the count of nonzeros in D(100)? It happens whenever n is a power of 10.

    fprintf('%15s %12s\n','n','nnz(D(n))')
    for n = 10.^(0:4)
        fprintf('%15d %12d\n',n, nnz(D(n)))
    end

              n    nnz(D(n))
              1            5
             10          317
            100        31417
           1000      3141549
          10000    314159053

O.E.I.S.

A classic problem, described in the Online Encyclopedia of Integer Sequences, asks how many points with integer coordinates lie within a disc of increasing radius. Our nonzero count provides the answer.

    fprintf('%15s %8s\n','n','a(n)')
    for n = [1:15  99:101  499:501  999:1001]
        if mod(n,100) == 99
            fprintf('%15s %8s\n','-','-')
        end
        a(n) = nnz(D(n));
        fprintf('%15d %8d\n',n,a(n))
    end

              n     a(n)
              1        5
              2       13
              3       29
              4       49
              5       81
              6      113
              7      149
              8      197
              9      253
             10      317
             11      377
             12      441
             13      529
             14      613
             15      709
              -        -
             99    30757
            100    31417
            101    32017
              -        -
            499   782197
            500   785349
            501   788509
              -        -
            999  3135157
           1000  3141549
           1001  3147833

R

Taking the reciprocals of the matrix entries, and reducing the range of the anonymous index, produces a matrix that behaves a bit like the Hilbert matrix, hilb(n).

    R = @(n) 1./((1:n).^2 + (1:n)'.^2);

Here are the 5-by-5's.

    format rat
    R5 = R(5)
    H5 = hilb(5)

R5 =

       1/2            1/5            1/10           1/17           1/26    
       1/5            1/8            1/13           1/20           1/29    
       1/10           1/13           1/18           1/25           1/34    
       1/17           1/20           1/25           1/32           1/41    
       1/26           1/29           1/34           1/41           1/50    


H5 =

       1              1/2            1/3            1/4            1/5     
       1/2            1/3            1/4            1/5            1/6     
       1/3            1/4            1/5            1/6            1/7     
       1/4            1/5            1/6            1/7            1/8     
       1/5            1/6            1/7            1/8            1/9     

Condition

Going away from the diagonal, the elements of R(n) decay more rapidly than those of hilb(n), so R(n) is better conditioned than hilb(n).

    format short e
    fprintf('%15s %12s %12s\n','n','cond R','cond H')
    for n = 1:12
        fprintf('%15d %12.2e %12.2e\n',n,cond(R(n)),cond(hilb(n)))
    end

              n       cond R       cond H
              1     1.00e+00     1.00e+00
              2     1.53e+01     1.93e+01
              3     2.04e+02     5.24e+02
              4     2.59e+03     1.55e+04
              5     3.21e+04     4.77e+05
              6     3.89e+05     1.50e+07
              7     4.67e+06     4.75e+08
              8     5.54e+07     1.53e+10
              9     6.53e+08     4.93e+11
             10     7.65e+09     1.60e+13
             11     8.92e+10     5.22e+14
             12     1.04e+12     1.62e+16

Extra Credit

What is the rank of Q(n)? Why? See a paper in SIAM Review by Strang and Moler.

Why is the table of values for nnz(D(10^k)) so short? How might you extend this table?

Investigate R(n). Is it positive definite? What are its eigenvalues? What is its inverse? What is the sign pattern of the elements of its inverse? For what values of n can you compute the inverse reliably using floating point arithmetic? How does all this compare with hilb(n) and invhilb(n) ?

Comments in the Comments, or in email to me, are welcome.

Get the MATLAB code

Published with MATLAB® R2022a