The Soma Cube, Again
The Soma Cube brings back memories.
Contents
Piet Hein
Piet Hein (1905-1996) was an extraordinary Danish inventor, mathematician, poet and philosopher. He invented the Soma Cube puzzle in 1933. I wrote a blog post about Hein and some of his creations several years ago, Soma Cube 2016.
The Soma Cube puzzle has seven pieces. One of them is a V-shaped piece made from three cubelets. The other six pieces are L, T, Z, R, S, and Y with four cubelets each. That's a total of 27 cubelets, just enough to make a 3-by-3-by-3 cube. Sound familiar?
Bill McKeeman
Bill McKeeman and I were buddies in grad school. He was a professor at U. C. Santa Cruz for a while, and then at the ill-fated Wang Institute of Graduate Studies in Tyngsborough, Mass. He worked for DEC in New Hampshire for a long time, taught compilers at Dartmouth, and even consulted for the MathWorks. As an exercise to learn MATLAB, he wrote the modern version of our why command.
The original soma demo
Bill and I became obsessed with the Soma cube after Martin Gardiner described the puzzle in his Scientific American column. You may not have noticed it before, but one of Bill's programs, soma, is in the MATLAB demos directory. Bill generated all of the 240 distinctly different puzzle solutions and stored them in a 240-by-27 matrix, demos/somasols. His program lets you page through the solutions.
A new Soma demo
My new Soma code uses technology from Qube, the digital Rubik's Cube simulator, to plot the 240 solutions. Here are the seven Soma pieces, surrounding an animation stepping through every tenth solution.
Do you recognize the colors?
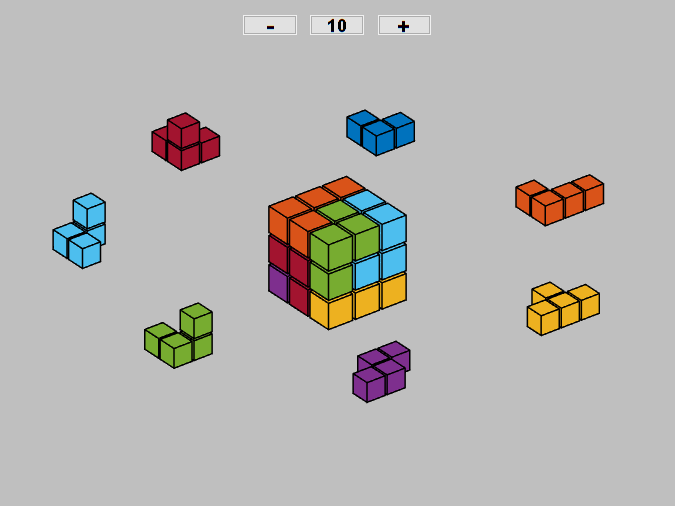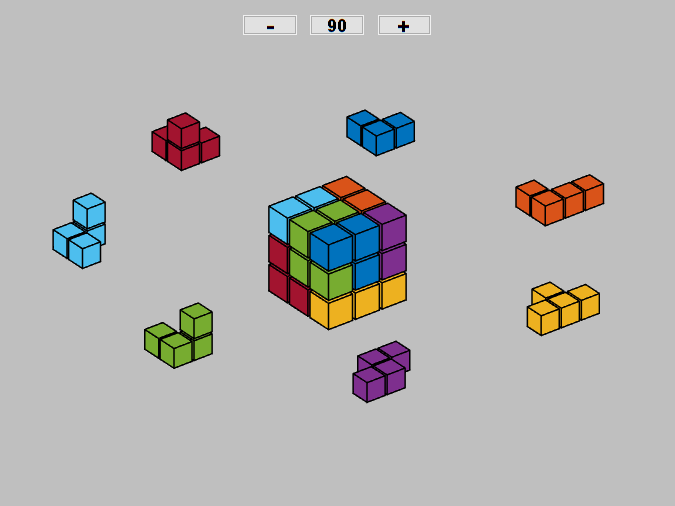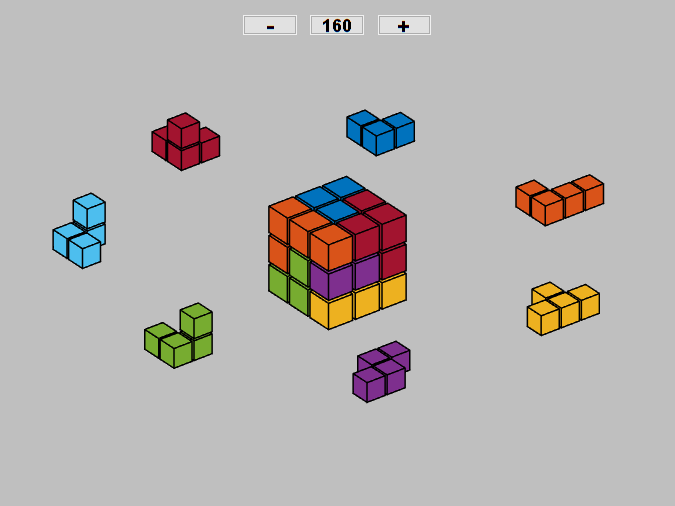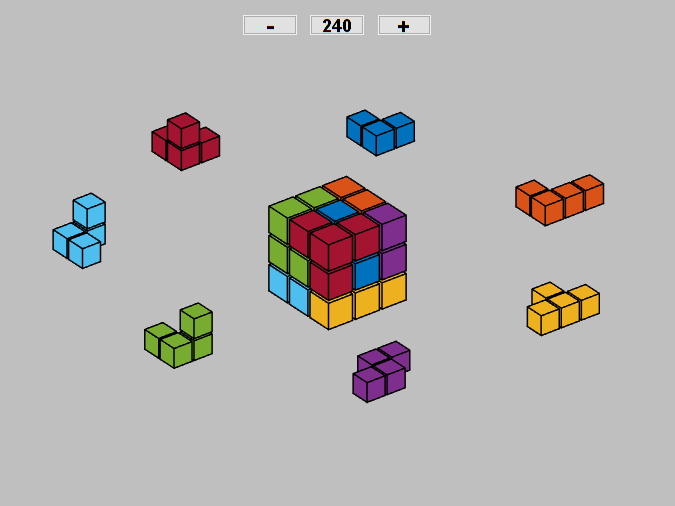
Software
Soma is available from this link. You already have somasols, but another copy is available from this link.
Update
I have combined my new display code and McKeeman's old program that finds all the solutions. The self-extracting archive is available at <https://blogs.mathworks.com/cleve/files/Soma_osf.m>
Get
the MATLAB code
Published with MATLAB® R2022b
