A Million Dollar Matrix

The twenty-second Householder Symposium on Numerical Linear Algebra is this week, June 8 - June 13, 2025 at Cornell. My talk on Wednesday had the provocative title "A Million-Dollar Matrix". A PDF of the slides available at link_1. The talk covers posts in the Cleve's Corner blog last fall. link_2, link_3, link_4.

Contents

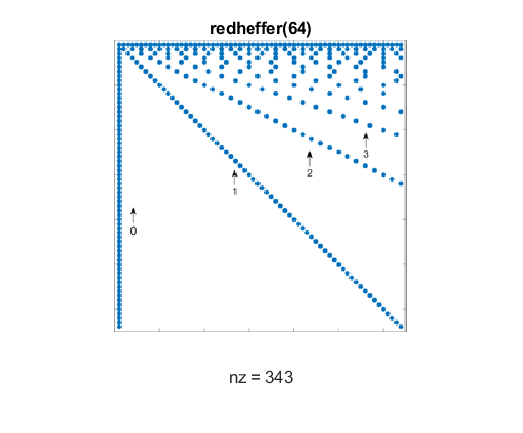
Redheffer Matrix

Ray Redheffer (1921-2005) was a professor of mathematics at UCLA from 1950 until 2000. The Redheffer matrix, which he introduced in 1977, is n-by-n, with elements

   R(k,j) = 1, if j = 1 or k divides j,
          = 0, otherwise

Here is a spy plot for n = 64. The nonzero elements lie in the first column and on diagonals with integer-valued slopes.

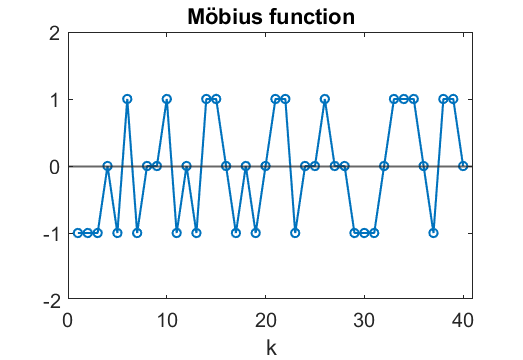
Möbius Function

August Möbius (1790-1868) was an eminent 19th-century German mathematician. His Möbius function is a fundamental tool in the study of prime numbers.

   mu(k) = 1 if k has an even number of distinct prime factors,
         = 0 if k has a repeated prime factor,
         = -1 if k has an odd number of distinct prime factors

Mertens Function

Franz Mertens (1840-1927) was born in the Grand Duchy of Posen in the Kingdom of Prussia, which is now Poland. He lived much his life in Vienna, Austria. The Mertens function is the cumulative sum of the Möbius function.

$$ M(n) = \sum_{k = 1}^{n} \mu(k) $$

M(n) is a running count of the integers that have an even number of prime factors, minus those with an odd number of prime factors.

Redheffer = Mertens

The determinant of the Redheffer matrix is equal to the Mertens function.

det(R(n)) = M(n)

Plots of M(n) are also plots of det(R(n)).

Mertens Conjecture

How fast does M(n) grow as n increases? Here are plots of M(n) for n in powers of 10 from n = 10 to n = 10^8, together with plots of sqrt(n) and -sqrt(n).

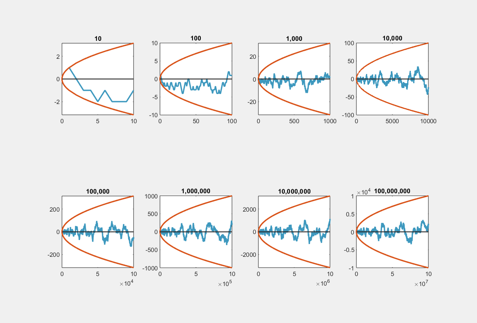
We see that, at least for n < 10^8,

   |M(n)| < √n

The Mertens conjecture is that this inequality holds for all n as n → ∞. This conjecture is of interest because it implies the Riemann hypothesis.

Riemann Hypothesis

The Riemann hypothesis has been called the “Most important unsolved problem in mathematics". Its resolution is the objective of a Clay Millenium Prize valued at one-million dollars. The hypothesis, proposed by G. F. Bernard Riemann in 1859, concerns the zeta function ζ(z) and the location of its zeros.

Riemann Computations

Computation of the first N non-trivial zeros of ζ(s).

                authors                    year                     N
   ____________________________________    ____    __________________
   Riemann                                 1854                     ?
   Gram                                    1903                    10
   Backlund                                1914                    79
   Hutchinson                              1925                   138
   Titchmarsh                              1936                 1,041
   Turing                                  1953                 1,104
   Lehmer                                  1956                25,000
   Meller                                  1958                35,337
   Lehman                                  1966               250,000
   Rosser, Yohe, Schoenfield               1969             3,502,500
   Brent                                   1977            40,000,000
   Brent                                   1979            81,000,001
   Brent, Van_de_Lune, Te_Riele, Winter    1982           200,000,001
   Van_de_Lune, Te_Riele, Winter           1986         1,500,000,001
   Van_de_Lune                             2001       100,000,000,000
   Wedeniwski                              2003       250,000,000,000
   Gourdon                                 2004    10,000,000,000,000

$1M

The Mertens conjecture

  |M(n)| < √n

implies the Riemann hypothesis and is worth $1M.

So, a proof that

  |det(R(n)| < √n

would earn R the title "Million-Dollar Matrix".

Spoiler

The Mertens conjecture is false.

Andrew Odlyzko and Herman te Riele (1985) prove

  limsup n→∞ M(n)/√n > 1.06

This proves the existence of infinitely many values of n for which

  |det(R(n))| > 1.06 √n

The proof is indirect. Nobody knows an actual value of n. Estimates are

  n >> 10^30

Redheffer Matrix

Even though it is not worth a million dollars, Nick Higham included the Redheffer matrix in the original MATLAB gallery. The command

  help private/redheff

says

  A has N-FLOOR(LOG2(N))-1 eigenvalues equal to 1,
  a real eigenvalue approximately SQRT(N),
  a negative eigenvalue approximately -SQRT(N),
  and the remaining eigenvalues are provably "small".

For n = 64, this becomes

  R(64) has 57 eigenvalues equal to 1,
  a real eigenvalue approximately 8.0,
  a negative eigenvalue approximately -8.0,
  and the remaining eigenvalues are provably "small".

Eigenvalues

The eigenvalues of R(64) are

   eig(redheffer(64))

   10.0445 + 0.0000i
   -5.5442 + 0.0000i
    0.0726 + 0.0000i
    0.3213 + 0.4487i
    0.3213 - 0.4487i
    0.8923 + 0.1262i
    0.8923 - 0.1262i

   followed by

    1.0000 + 0.0000i

   repeated 57 times.

Characteristic polynomial

The characteristic polynomial of R(64) is

  p(z) * (z – 1)^57

where

  p(z) = z^7 - 7^z^6 - 42*z^5 + 127*z^4 - 130*z^3 + 67*z^2 - 18*z + 1

Jordan Canonical Form

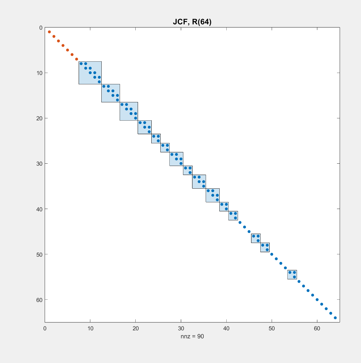
Code

typemobius.m

function mu = mobius(n)
    % mu = mobius(n)
    mu = ones(1,n);
    mu(1) = -1;
    for p = primes(n)
        mu(p^2:p^2:n) = 0;
        mu(p:p:n) = -mu(p:p:n);
    end
end

typemertens.m

function M = mertens(n)
    % M = mertens(n)
    mu = mobius(n);
    M = cumsum([1 mu(2:n)]);
end

typeredheffer.m

function R = redheffer(n)
    % R = redheffer(n)
    k = 1:n;
    R = mod(k,k') == 0;
    R(:,1) = 1;
    R = double(R);
end

typesparse_redheffer.m

function S = sparse_redheffer(n)
    % S = sparse_redheffer(n)
    j(1:n) = (1:n)';
    k(1:n) = 1;
    m = n;
    for i = 2:n
        t = [1 i:i:n]';
        p = length(t);
        j(m+(1:p)) = t;
        k(m+(1:p)) = i;
        m = m+p;
    end
    S = sparse(k,j,1,n,n);
end

Sparse Redheffer

     n    tictoc            bytes            nnz      sparsity      det    |det|/√n
  10^1     0.000              664             36     0.3600000       -1      0.316
  10^2     0.000           10,104            581     0.0581000        1      0.100
  10^3     0.003          137,096          8,068     0.0080680        2      0.063
  10^4     0.021        1,738,680        103,667     0.0010367      -23      0.230
  10^5     0.216       21,067,992      1,266,749     0.0001267      -48      0.152
  10^6     2.515      247,520,536     14,970,033     0.0000150      212      0.212
  10^7    32.429    2,843,605,816    172,725,363     0.0000017     1037      0.328

Five Ways

typefiveways

function M = fiveways(n)
    % Five Ways to Compute the Mertens/Redheffer Function 
    %1 
        R = redheffer(n);
        M(1) = det(R);
    %2 
        R =  sparse_redheffer(n);
        [L,U,P,Q] = lu(R);
        M(2) = det(L)*det(U)*det(P)*det(Q);
    %3
        R =  sparse_redheffer(n);
        R(:,[1 n]) = R(:,[n 1]);
        M(3) = -det(R);
    %4
        R =  sparse_redheffer(n);
        T = R(2:n,2:n);
        e = ones(1,n-1);
        M(4) = 1 - e*(T\e');
    %5 
        mu = mobius(n);
        cmu = cumsum([1 mu(2:end)]);
        M(5) = cmu(n);
end   

Complexity

     redheffer function  dets  complexity      M

  #1 full      gallery     1   n^3             1
  #2 sparse    lu          4   n*log(n)^2      1
  #3 sparse    swap        1   n*log(n)^2      1
  #4 sparse    \           0   n*log(n)        1
  #5 none      primes      0   n*log(log(n))  many

Timing

         2e4     2e5     2e6     2e7

   #1   26.33     -       -       -
   #2    0.36   21.53     -       -
   #3    0.08    1.29   16.71     -
   #4    0.05    0.57    6.32   70.85
   #5    0.01    0.03    0.27    3.18

               Time (seconds)

References

Thanks

Get the MATLAB code

Published with MATLAB® R2024b